Introduction to Algorithms

Informally, an algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. An algorithm is thus a sequence of computational steps that transform input into the output.

An algorithm is considered correct if, for every input instance, it halts with the correct output. We say that a correct algorithm solves the given computational problem. Contrary to common belief, incorrect algorithms can sometimes be useful, if we can control their error rate.

\(\textcolor{#FF90BC}{\Longrightarrow}\) An algorithm can be viewed as a tool for solving a well-specified computational problem

Efficiency

When assessing the efficiency of algorithms—comparing whether algorithm A is more efficient than algorithm B—we should focus on counting fundamental operations rather than measuring time. Performance is typically expected to vary based on the size of the input. As defined by [CLRS09] “we are concerned with how the running time of an algorithm increases in the size of the input in the limit, as the size of the input increases without bound.”

\(\textcolor{#FF90BC}{\Longrightarrow}\) \(O(\cdot)\) Upper bound \(\quad | \quad \Omega(\cdot)\) Lower Bound \(\quad | \quad \Theta(\cdot)\) Both

\(\textcolor{#FF90BC}{\Longrightarrow}\) \(o(\cdot)\) Strict upper bound \(\quad | \quad \omega(\cdot)\) Strict lower bound

Two primary measures determine algorithm efficiency: time complexity and space complexity.

Space Complexity

The amount of time an algorithm takes to run as a function of the input size.

Time Complexity

The amount of memory an algorithm requires to run as a function of the input size.

When evaluating either type of complexity—time or space—we utilize asymptotic notation, which we define briefly below:

• \(\Theta\)-notation: Represents the asymptotically tight bound of an algorithm’s complexity. It defines functions that grow at the same rate asymptotically.

• \(O\)-notation: Denotes the upper bound of an algorithm’s complexity. It signifies the worst-case scenario of the algorithm’s growth rate.

• \(\Omega\)-notation: Indicates the lower bound of an algorithm’s complexity. It defines the best-case scenario of the algorithm’s growth rate.

• \(o\)-notation: Describes a stricter upper bound than \(O\)-notation. It denotes functions that grow faster than a given function but not asymptotically tight.

• \(\omega\)-notation: Denotes a stricter lower bound than \(\Omega\)-notation. It signifies functions that grow faster than a given function but not asymptotically tight.

For example, we represent notations such as \(O(n)\), \(O(2^n)\), \(O(n \log n)\), \(O(n^2)\), \(O(\log n)\), and others. The distinctions between these functions can be visualized through plots, as illustrated in the figure below.

See Figure for a visual comparison of complexity graph curves.

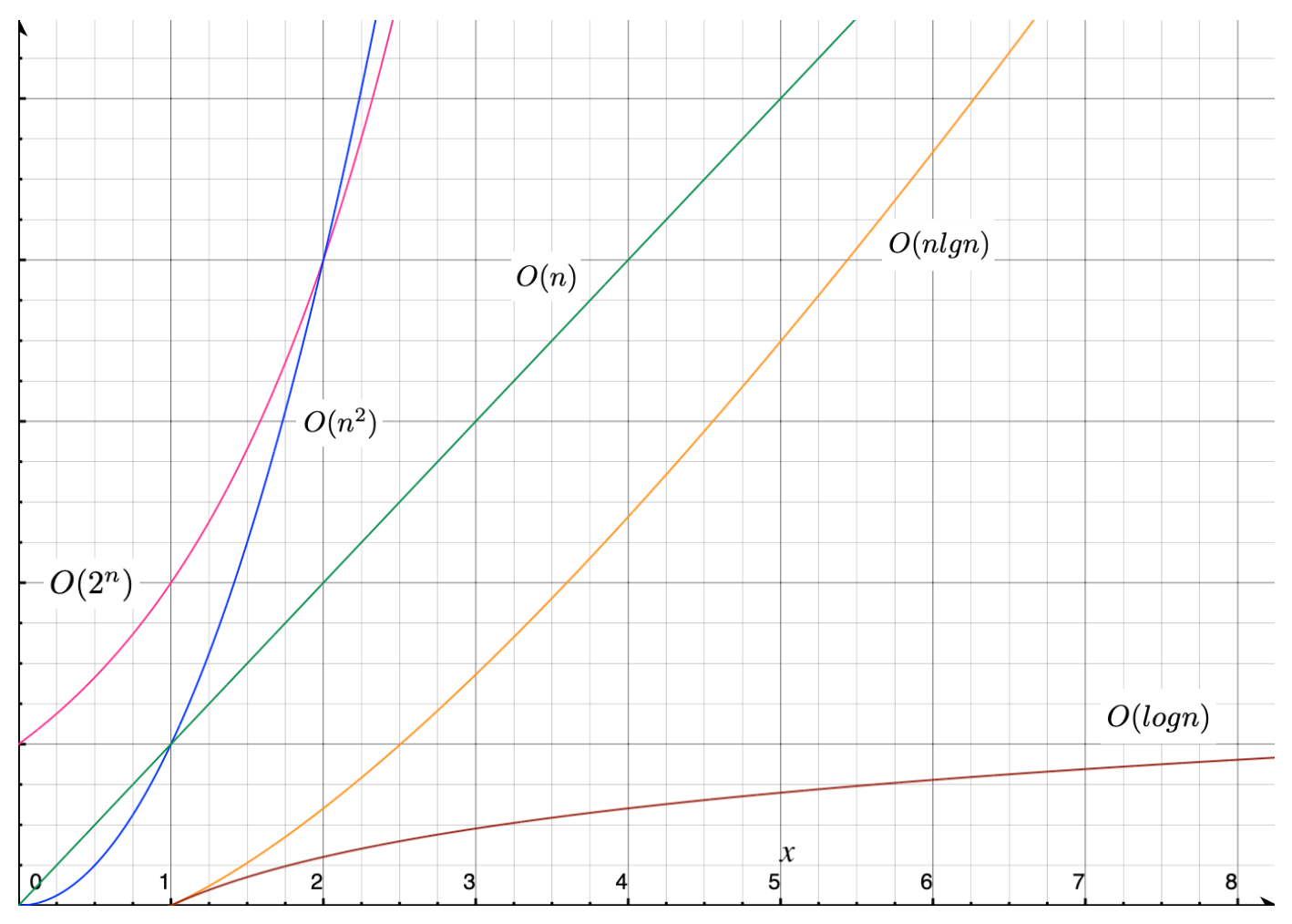
Fig. 1 Comparison of complexity graph curves.