Dynamic Programming#
A dynamic-programming algorithm solves each subproblem just once and then saves its answer in a table, thereby avoiding the work of recomputing the answer every time it solves each subproblem. Dynamic programming applies when the subproblems overlap, that is, when subproblems share subsubproblems. In this context, a divide-and-conquer algorithm does more work than necessary, repeatedly solving the common subproblems. When developing a dynamic-programming algorithm, we follow a sequence of four steps:
Characterize the structure of an optimal solution
Recursively define the value of an optimal solution
Compute the value of an optimal solution, typically in a bottom-up fashion
Construct an optimal solution from computed information
Solving the problem initially using divide and conquer is not a bad idea, considering that we optimize the code logic afterwards.
0/1 Knapsack#
Example: Imagine we are going to the supermarket, and we want to buy a selection of products to take with us to the park. We have only one backpack with a certain capacity, and we want to maximize the total value of the products we can fit into our backpack. The condition here is that we can only choose one product of each type.
We enter a supermarket with a backpack that has a capacity of \( m = 50 \) units. There are \( n = 3 \) products available:
Product 1: cost \( c_1 = 60 \), weight \( w_1 = 10 \)
Product 2: cost \( c_2 = 100 \), weight \( w_2 = 20 \)
Product 3: cost \( c_3 = 120 \), weight \( w_3 = 30 \)
The goal is to determine the maximum value of the backpack when products are not allowed to be fractioned. In this example, we should take Product 2 and Product 3 to maximize the total value. Thus, the total value would be 220.
Algorithms#
There are several methods to solve the knapsack problem. With that in mind, let’s demonstrate some algorithms and illustrate each using the following:
\(weights = [1, 2, 3]\)
\(values = [6, 10, 12]\)
\(capacity = 5\)
Naive Recursive Algorithm#
\(\textcolor{#FFC0D9}{\Longrightarrow}\) Time Complexity of \(O(2^n)\) | Space Complexity of \(O(n)\), where \(n\) is the number of items
def knapsack_helper(level, capacity, weights, values):
if level == len(values):
return 0
# Exclude the item, as including it would exceed the capacity of our backpack.
if weights[level] > capacity:
return knapsack_helper(level + 1, capacity, weights, values)
profit_with = values[level] + knapsack_helper(
level + 1, capacity - weights[level], weights, values
)
profit_without = knapsack_helper(level + 1, capacity, weights, values)
return max(profit_with, profit_without)
def knapsack_naive(capacity, weights, values):
return knapsack_helper(0, capacity, weights, values)
# Example usage:
weights = [1, 2, 3]
values = [6, 10, 12]
capacity = 5
print("Answer: ", knapsack_naive(capacity, weights, values))
Answer: 22
Memoization Algorithm#
\(\textcolor{#FFC0D9}{\Longrightarrow}\) Time Complexity of \(O(n \cdot W)\) | Space Complexity of \(O(n \cdot W)\), where \(W\) is the knapsack capacity and \(n\) the number of items
Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and reusing them when the same inputs occur again. This avoids the need to recompute results for the same inputs, significantly improving the time complexity in many cases.
Key Concepts of Memoization#
Cache Storage: Memoization involves creating a cache (typically a dictionary or array) where the results of function calls are stored. The cache keys are the function arguments, and the cache values are the computed results.
Function Modification: The original function is modified to first check if the result for a given input is already in the cache. If it is, the cached result is returned immediately, bypassing the computation. If not, the function computes the result, stores it in the cache, and then returns it.
Time Complexity Improvement: By avoiding redundant calculations, memoization can transform algorithms with exponential time complexity into those with polynomial time complexity. This is particularly effective in dynamic programming, where overlapping subproblems are common.
Steps to Implement Memoization#
Identify the Overlapping Subproblems: Determine the parts of the algorithm where the same calculations are repeated multiple times.
Create a Cache: Initialize a data structure to store the results of these subproblems. A dictionary is commonly used for its efficient look-up time.
Modify the Function: Before performing any calculation, the function should check if the result is already in the cache. If it is, return the cached result. If not, compute the result, store it in the cache, and then return it.
This optimizes the naive approach using a memoization technique, significantly improving the time complexity to \(O(n \cdot m)\).
def knapsack_helper_memo(level, capacity, weights, values, memo):
if level == len(values):
return 0
if (level, capacity) in memo:
return memo[(level, capacity)]
# Exclude the item, as including it would exceed the capacity of our backpack.
if weights[level] > capacity:
memo[(level, capacity)] = knapsack_helper_memo(
level + 1, capacity, weights, values, memo
)
return memo[(level, capacity)]
profit_with = values[level] + knapsack_helper_memo(
level + 1, capacity - weights[level], weights, values, memo
)
profit_without = knapsack_helper_memo(level + 1, capacity, weights, values, memo)
memo[(level, capacity)] = max(profit_with, profit_without)
return memo[(level, capacity)]
def knapsack_memo(capacity, weights, values):
memo = {}
return knapsack_helper_memo(0, capacity, weights, values, memo)
# Example usage:
weights = [1, 2, 3]
values = [6, 10, 12]
capacity = 5
print("Answer: ", knapsack_memo(capacity, weights, values))
Answer: 22
Dynamic Programming Algorithm#
\(\textcolor{#FFC0D9}{\Longrightarrow}\) Time Complexity of \(O(n \cdot W)\) | Space Complexity of \(O(n \cdot W)\), where \(W\) is the knapsack capacity and \(n\) the number of items
This approach uses a 2D array to compute the solution iteratively, also achieving a time complexity of \(O(n \cdot m)\).
The table in Figure below depicts the dynamic programming table for a knapsack problem with weights [1, 2, 3], values [6, 10, 12], and a capacity of 5. In this table:
The rows represent the index of items, including a row for no items (index 0, 1, or 2).
The columns correspond to knapsack capacities ranging from 0 to the maximum capacity.
Each cell \(dp[i][w]\) shows the maximum profit that can be obtained using the first \(i\) items with a knapsack capacity of \(w\).
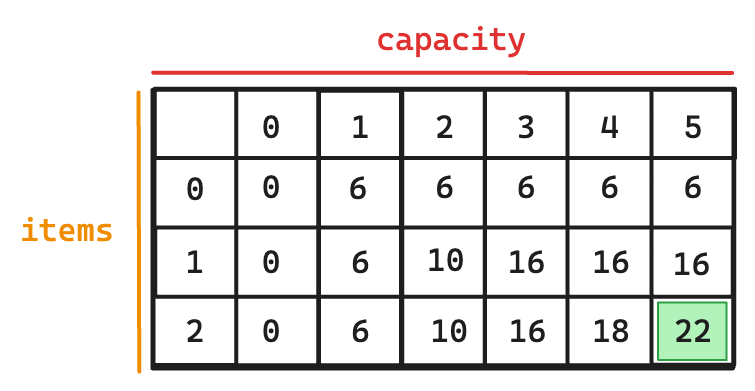
Fig. 10 Dynamic programming table for the 0/1 Knapsack problem with weights [1, 2, 3], values [6, 10, 12], and capacity of 5. Each cell \(dp[i][m]\) represents the maximum profit for the first \(i\) items with a capacity \(m = 5\)#
def knapsack_dp(values, weights, capacity):
N = len(values)
W = capacity
dp = [[0] * (W + 1) for _ in range(N)]
# Fill the first row based on the first item's weight and value
for c in range(W + 1):
if weights[0] <= c:
dp[0][c] = values[0]
for i in range(1, N):
for c in range(1, W + 1):
skip = dp[i - 1][c]
include = 0
if c >= weights[i]:
include = values[i] + dp[i - 1][c - weights[i]]
dp[i][c] = max(include, skip)
print("The dp arrray: ", dp)
return dp[N - 1][W]
# Example usage:
weights = [1, 2, 3]
values = [6, 10, 12]
capacity = 5
print("Answer: ", knapsack_dp(values, weights, capacity))
The dp arrray: [[0, 6, 6, 6, 6, 6], [0, 6, 10, 16, 16, 16], [0, 6, 10, 16, 18, 22]]
Answer: 22
Animation for DP approach#
For a step by step animation on how the dynamic solution for the 0/1 knapsack problem please refer to the slides below
Unbounded Knapsack#
The unbounded knapsack problem is a variation of the classic 0/1 knapsack problem where you can use each item an unlimited number of times.
Given a set of items, each with a weight and a value, the goal is to determine the maximum value that can be obtained by putting items into a knapsack with a given capacity, with the additional constraint that an item can be chosen multiple times.
Problem Statement#
Input:
A list of item weights: \(weights = [w_1, w_2, \ldots, w_n]\)
A list of item values: \(values = [v_1, v_2, \ldots, v_n]\)
The capacity of the knapsack: \(capacity\)
Output:
The maximum value that can be achieved with the given capacity, allowing multiple occurrences of each item.
Algorithms#
Let’s consider an example with the following inputs:
\(weights = [1, 2, 3]\)
\(values = [6, 10, 12]\)
\(capacity = 5\)
We need to find the maximum value that can be achieved with a knapsack capacity of 5 using the items multiple times.
Naive Recursive approach#
\(\textcolor{#FFC0D9}{\Longrightarrow}\) Time Complexity of \(O(2^n)\) | Space Complexity of \(O(n \cdot W)\), where \(W\) is the knapsack capacity and \(n\) the number of items
def unbound_knapsack(level, values, weights, capacity):
if level == len(values) or capacity <= 0:
return 0
if weights[level] > capacity:
return unbound_knapsack(level + 1, values, weights, capacity)
# We're deciding to add the element [0]
profit_with = values[level] + unbound_knapsack(
level, values, weights, capacity - weights[level]
)
# We're deciding to NOT add the element [0]
profit_without = unbound_knapsack(level + 1, values, weights, capacity)
# Choose which one retrieves the biggest value
return max(profit_with, profit_without)
def unbound_knapsack_helper(values, weights, capacity):
return unbound_knapsack(level=0, values=values, weights=weights, capacity=capacity)
# Example usage:
weights = [1, 2, 3]
values = [6, 10, 12]
capacity = 5
print("Answer: ", unbound_knapsack_helper(values, weights, capacity))
Answer: 30
Memoization#
\(\textcolor{#FFC0D9}{\Longrightarrow}\) Time Complexity of \(O(n \cdot W)\) | Space Complexity of \(O(n \cdot W)\), where \(W\) is the knapsack capacity and \(n\) the number of items
As explained before, memoization can help us to optimize our problem. Let’s apply it to our unbound knapsack recursive algorithm.
def unbound_knapsack_memo(level, values, weights, capacity, memo):
if level == len(values) or capacity <= 0:
return 0
if (level, capacity) in memo:
return memo[(level, capacity)]
if weights[level] > capacity:
return unbound_knapsack_memo(level + 1, values, weights, capacity, memo)
# We're deciding to add the element [0]
profit_with = values[level] + unbound_knapsack_memo(
level, values, weights, capacity - weights[level], memo
)
# We're deciding to NOT add the element [0]
profit_without = unbound_knapsack_memo(level + 1, values, weights, capacity, memo)
# Choose which one retrieves the biggest value
profit = max(profit_with, profit_without)
memo[(level, capacity)] = profit
return profit
def unbound_knapsack_memo_helper(values, weights, capacity):
memo = {}
return unbound_knapsack_memo(
level=0, values=values, weights=weights, capacity=capacity, memo=memo
)
# Example usage:
weights = [1, 2, 3]
values = [6, 10, 12]
capacity = 5
print("Answer: ", unbound_knapsack_memo_helper(values, weights, capacity))
Answer: 30
Dynamic Programming#
\(\textcolor{#FFC0D9}{\Longrightarrow}\) Time Complexity of \(O(n \cdot W)\) | Space Complexity of \(O(W)\), where \(W\) is the knapsack capacity and \(n\) the number of items
To solve the unbounded knapsack problem, dynamic programming is often used. The idea is to build a solution iteratively using previously computed results.
Initialization:
Create a table
dpwheredp[i]will store the maximum value achievable with knapsack capacityi.
Iterative Solution:
Iterate through all capacities from
0tocapacity.For each capacity, iterate through all items to check if it can be included in the current capacity. Update the
dptable accordingly.
The dynamic programming formula for the unbounded knapsack problem is:
where w_j is the weight of the item and v_j is the value of the item.
def unbound_knapsack_dp(values, weights, capacity):
N, W = len(values), capacity + 1
dp = [[0] * W for _ in range(N)]
# Initialize for boundary conditions
for _capacity in range(W):
dp[0][_capacity] = (_capacity // weights[0]) * values[0]
for i in range(1, N):
for _capacity in range(W):
profit_without = dp[i - 1][_capacity] # profit without including item i
profit_with = 0
if _capacity >= weights[i]: # profit including item i
profit_with = values[i] + dp[i][_capacity - weights[i]]
dp[i][_capacity] = max(profit_without, profit_with)
print(f"The dp array: {dp}")
return dp[N - 1][W - 1]
# Example usage:
weights = [1, 2, 3]
values = [6, 10, 12]
capacity = 5
print("Answer: ", unbound_knapsack_dp(values, weights, capacity))
The dp array: [[0, 6, 12, 18, 24, 30], [0, 6, 12, 18, 24, 30], [0, 6, 12, 18, 24, 30]]
Answer: 30
Complexity Table#
Knapsack Type |
Solution Type |
Time Complexity |
Space Complexity |
|---|---|---|---|
0/1 Knapsack |
Recursive Solution |
\(O(2^n)\) |
\(O(n)\) |
0/1 Knapsack |
Memoization Recursive Solution |
\(O(n \cdot W)\) |
\(O(n \cdot W)\) |
0/1 Knapsack |
DP Solution |
\(O(n \cdot W)\) |
\(O(n \cdot W)\) |
Unbounded Knapsack |
Recursive Solution |
\(O(2^n)\) |
\(O(n)\) |
Unbounded Knapsack |
Memoization Recursive Solution |
\(O(n \cdot W)\) |
\(O(n \cdot W)\) |
Unbounded Knapsack |
DP Solution |
\(O(n \cdot W)\) |
\(O(W)\) |
